5.1.3 Satisfaction, Assignments

We cannot give a direct inductive definition of truth. Truth is a relation that holds between sentences and models. But the matrix of a quantified sentence typically won't be a sentence. For example, 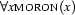is a sentence, but its matrix 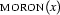is not. Thus an inductive truth definition given solely in terms of sentences couldn't explain why would be true in a model, for there are no sentential subformulae for such a definition to refer to.

An indirect Approach

So instead, we're going to proceed indirectly by defining a three place relation-called satisfaction-which holds between a formula, a model, and an assignment of values to variables. Given a model 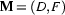, an assignment of values in 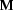to variables (or more simply, an assignment in 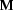) is a function from the set of variables to 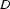. Assignments are a technical aid that tells us what free variables stand for. By making use of assignment functions, we can inductively interpret arbitrary formulae in a natural way, which will make it possible for us to define the concept of truth for sentences.