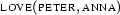1.2.3 Building Formulas
Terms
Let's suppose we've composed a certain vocabulary. How do we mix these ingredients together? That is, what is the syntax of first-order languages? First of all, we define a first-order term  to be any constant or any variable. Roughly speaking, terms are the noun phrases of first-order languages: constants can be thought of as first-order counterparts of proper names, and variables as first-order counterparts of pronouns.
to be any constant or any variable. Roughly speaking, terms are the noun phrases of first-order languages: constants can be thought of as first-order counterparts of proper names, and variables as first-order counterparts of pronouns.
Atomic Formulas
We can then combine our ``noun phrases'' with our ``predicates'' (meaning, the various relation symbols in the vocabulary) to form what we call atomic formula s:
If  is a relation symbol of arity
is a relation symbol of arity  , and
, and 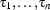 are terms, then
are terms, then 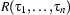 is an atomic formula.
is an atomic formula.
Intuitively, an atomic formula is the first-order counterpart of a natural language sentence consisting of a single clause (that is, a simple sentence). So what does a formula like 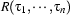 actually mean? As a rough translation, we could say that the entities that are named by the terms
actually mean? As a rough translation, we could say that the entities that are named by the terms 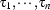 stand in a relationship that is named by the symbol
stand in a relationship that is named by the symbol  . An example will clarify this point:
. An example will clarify this point:
What's meant by this formula is that the entity named 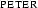 stands in the relation denoted by
stands in the relation denoted by 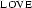 to the entity named
to the entity named 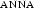 - or more simply, that Peter loves Anna.
- or more simply, that Peter loves Anna.
Complex Formulas
Now that we know how to build atomic formulas, we can define more complex ones as well. The following inductive definition tells us exactly what kinds of well-formed formula s (or wffs, or simply formulas) we can form.
All atomic formulas are wffs.
If
 and
and 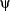 are wffs then so are
are wffs then so are 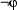 ,
, 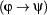 ,
, 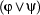 , and
, and 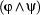 .
.If
 is a wff, and x is a variable, then both
is a wff, and x is a variable, then both  and
and 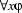 are wffs. (We call
are wffs. (We call  the matrix or scope of such wffs.)
the matrix or scope of such wffs.)Nothing else is a wff.
Roughly speaking, formulas built using 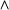 ,
, 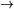 ,
, 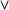 and
and  correspond to the natural language expressions ``... and ...'', ``if ... then ...'', ``... or ...'', and ``it is not the case that ...'', respectively. First-order formulas of the form
correspond to the natural language expressions ``... and ...'', ``if ... then ...'', ``... or ...'', and ``it is not the case that ...'', respectively. First-order formulas of the form  and
and 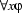 correspond to natural language expressions of the form ``some...'' or ``all...''.
correspond to natural language expressions of the form ``some...'' or ``all...''.