3.2.8 Relating Constraint Graphs and Lambda-Structures

We've just seen pictures that gave us an intuitive idea of how 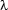-structures relate to constraint graphs. Let's now frame our intuition into a more formal definition. We can say that a constraint graph describe s a 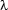-structure if it's possible to embed the tree fragments into the 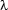-structure. (In this case we also say that the 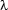-structure is a solution of the constraint graph.) That is, we must be able to map the nodes of the constraint graph to nodes of the 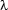-structure in a way that satisfies the following conditions:

1. Any node that has a label in the graph must have the same label in the 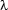-structure.

2. No two nodes that have a label in the graph must be mapped to the same node in the 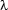-structure.

3. Any two nodes connected with a solid edge or a binding edge in the graph must be connected in the same way in the 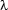-structure.

4. Whenever there is a dominance edge from a node 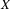to a node in the graph, there must be a path from 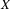to using only solid edges in the 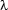-structure.

Intuitively again, embedding a constraint graph into a 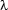-structure is a bit of a jigsaw puzzle: Overlay parts of the 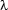-structure with matching tree fragments so that no two fragments overlap and all the dominances are respected. If you start with a constraint graph and want to construct 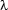-structures that it describes, the puzzle character comes out even more strongly, as you basically have to configure the tree fragments into a valid 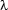-structure.

In the example, it is clearly possible to embed the fragments in the graph into each of the two 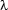-structures; the embeddings indicated by the colouring also respect the dominance requirements. Note that while different fragments do overlap at the borders, there never are any two labeled nodes that are mapped to the same node in the structure.