2.5 Lambda at Work

Beta-Reduce Afterwards

By now, we have seen all ingredients of our core system in detail, and we've provided almost all of the neccessary plug-ins for 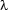-based semantic construction. Almost all: Because remember that we still need to post-process the semantic representations our grammar produces, meaning we have to 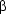-reduce them. Luckily, we already have the predicate betaConvert/2 from the last chapter at our avail for this purpose.

Plugging Together

What's next? Let's plug it all together and provide a user-interface! The predicate lambda/0 will be our driver predicate:

lambda :- readLine(Sentence), parse(Sentence,Formula), betaConvert(Formula,Converted), resetVars,vars2atoms(Formula), printRepresentations([Converted]).

parse(Sentence,Formula):- s2(Formula,Sentence,[]).

First, readLine(Sentence) reads in the input. Next, parse(Sentence,Formula) tests whether this input is accepted by our grammar as a sentence (the predicate simply calls our DCG to parse a phrase of category s2). If the input is a sentence, the 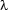-expression representing its meaning is returned in Formula. For example, for the input ``Tweety smokes.'', we get the output lambda(A, A@tweety)@lambda(B, smoke(B)). This expression is then 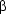-converted, and finally all remaining Prolog variables in it are replaced by atoms.

Check it out!

Our driver predicate lambda/0 is contained in the module lambda, which is the main module for 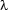-calculus. Below, we give a listing of all modules that are used by lambda. But before that, here is an example call for the sentence ``A therapist loves a siamese cat'':

lambda([a,therapist,loves,a,siamese,cat],Sem),write(Sem).

All modules used by lambda.pl

`lambda.pl`: View Download	The driver predicate; definition of the `combine`-rules and the lexical macros for -calculus.
`comsemOperators.pl`: View Download	Operator definitions.
`englishGrammar.pl`: View Download	The DCG-rules and the lexicon (using module `englishLexicon`). From here, the `combine`-rules and lexical macros defined by `lambda` are called.
`englishLexicon.pl`: View Download	The lexical entries for a small fragment of English.
`betaConversion.pl`: View Download	-conversion.
`comsemLib.pl`: View Download	Auxiliaries.
`signature.pl`: View Download	Generating new variables
`readLine.pl`: View Download	Reading the input from stdin.