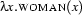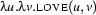1.4.1 Lambda-Abstraction
 -expressions are formed out of ordinary first order formulas using the
-expressions are formed out of ordinary first order formulas using the  -operator. We can prefix the
-operator. We can prefix the 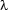 -operator, followed by a variable, to any first order formula or
-operator, followed by a variable, to any first order formula or 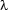 -expression. We call expressions with such prefixes
-expression. We call expressions with such prefixes 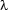 -abstraction s (or, more simply, abstractions). We say that the variable following a
-abstraction s (or, more simply, abstractions). We say that the variable following a 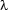 -operator is abstracted over . And we say that the variable abstracted over is (
-operator is abstracted over . And we say that the variable abstracted over is (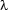 -)bound by its respective
-)bound by its respective 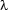 -operator within an abstraction, just as we say that a quantified variable is bound by its quantifier inside a quantification.
-operator within an abstraction, just as we say that a quantified variable is bound by its quantifier inside a quantification.
Abstractions
The following two are examples of 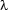 -abstractions:
-abstractions:
In the first example, we have abstracted over  . Thus the
. Thus the  in the argument slot of
in the argument slot of 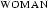 is bound by the
is bound by the 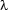 in the prefix. In the second example, we have abstracted twice: Once over
in the prefix. In the second example, we have abstracted twice: Once over  and once over
and once over  . So the
. So the  in the first argument slot of
in the first argument slot of 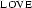 is bound by the first
is bound by the first 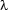 , and the
, and the  is bound by the second one.
is bound by the second one.
Missing Information
We will think of occurrences of variables bound by 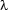 as placeholders for missing information: They serve us to mark explicitly where we should substitute the various bits and pieces obtained in the course of semantic construction. Let us look at our first example
as placeholders for missing information: They serve us to mark explicitly where we should substitute the various bits and pieces obtained in the course of semantic construction. Let us look at our first example 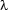 -expression again. Here the prefix
-expression again. Here the prefix 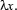 states that there is information missing in the formula following it (a one-place predication), and it gives this ``information gap'' the name
states that there is information missing in the formula following it (a one-place predication), and it gives this ``information gap'' the name  . The same way in our second example, the two prefixes
. The same way in our second example, the two prefixes  and
and 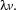 give us separate handles on each of the two information gaps in the following two-place predication.
give us separate handles on each of the two information gaps in the following two-place predication.